原题链接
题面大意翻译:
给定一系列数字。
可以在这列数字中取两个数a i a_i a i a j a_j a j i ≠ j i \neq
j i = j
取a i a_i a i x x x
将a i a_i a i a i x \frac{a_i}{x} x a i a j a_j a j a j ⋅ x a_j \cdot x a j ⋅ x
问是否能根据任意次操作,使得最后这列数字都相等。
例如:
[100,2,50,10,1]
取a 3 = 50 a_3 = 50 a 3 = 5 0 a 2 = 2 a_2 = 2 a 2 = 2 x = 5 x = 5 x = 5 a 3 a_3 a 3 a 3 x = 10 \frac{a_3}{x}=10 x a 3 = 1 0 a 2 a_2 a 2 a 2 ⋅ x = 10 a_2 \cdot x = 10 a 2 ⋅ x = 1 0
取a 1 = 100 a_1 = 100 a 1 = 1 0 0 a 5 = 1 a_5 = 1 a 5 = 1 x = 10 x = 10 x = 1 0 a 1 a_1 a 1 a 1 x = 10 \frac{a_1}{x}=10 x a 1 = 1 0 a 5 a_5 a 5 a 2 ⋅ x = 10 a_2 \cdot x = 10 a 2 ⋅ x = 1 0
在两次操作后,我们成功将这个列表的元素都变成了相同的数字。
我们只需要输出能否通过任意次操作来完成这个目标。
选定一个数的一个因子,让它自身除以这个因子,让一个别的数乘以这个因子。
抽象来看,可以看作是这个数的因子转移到了另一个数身上。
所以首先第一步就是把列表里的数字都拆成质因数的乘积。
虽然可以转移任意的因子,但拆成质因数后更好判断能不能转移。
如何判断可以完成目标呢?给个例子:
这个列表[125,8,27]
拆成质因数就是$$[55 5, 22 2, 33 3]$$
通过转移他们的质因数,我们可以把它变成$$[23 5,23 5,23 5]$$。
也就是变成了[30,30,30]。
注意到实际上就是将他们不同的质因数平均分配给n n n
所以我们可以只需要搜集质因数的个数,看最后的总个数是否是n的整数倍就可以了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 #define fi(i,l,r) for(int i=l;i<=r;i++) void divided (int x, unordered_map<int ,int >& umap) int i = 2 ; while (i * i <= x) { while (x % i == 0 ) { umap[i]++; x /= i; } i++; } if (x > 1 ) umap[x]++; return ; } void solve () int n; cin >> n; int a; unordered_map<int , int > umap; fi (i, 0 , n - 1 ) { cin >> a; divided (a, umap); } for (auto & e : umap) { if (e.second % n != 0 ) { cout << "NO\n" ; return ; } } cout << "YES\n" ; return ; } int main () ios::sync_with_stdio (0 ); cin.tie (0 ); int t; cin >> t; while (t--) { solve (); } return 0 ; }
原题链接
题目大意翻译:
给定一个列表,它需要被分成多个区块(blocks)。每个区块的第一个数字x x x x x x
可以删去这个列表的任意数字,问需要至少删除几个数字才能让这个列表满足以上条件。
例如:
[1,2,3,4,5]
删去1和5两个数字,列表可以被分为[[2,3,4]]。
[5,6,3,2]
删去任意数字都不能满足条件,只能全删了,回答是4。
这题可以用动态规划的思路来解决。
定义dp[i]存储的是要让从i → n i \to n i → n
如果选择删去第i i i dp[i] = dp[i+1] + 1。
如果不删的话就是dp[i] = dp[i+a[i]+1]。它作为序列头,自己自然就等于下个序列的头了。
特别的,当i+a[i]+1 > n时说明必须要删掉当前的数才能满足条件。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 void solve () int n; cin >> n; vector<int > a (n) , dp (n, n+1 ) ; fi (i, 0 , n - 1 ) { cin >> a[i]; } dp[n - 1 ] = 1 ; auto getNum = [&n, &dp](int x) { if (x > n) return n + 1 ; if (x == n) return 0 ; return dp[x]; }; for (int i = n - 2 ; i >= 0 ; --i) { dp[i] = min (dp[i + 1 ] + 1 , getNum (i + a[i] + 1 )); } cout << dp[0 ] << '\n' ; return ; } int main () ios::sync_with_stdio (0 ); cin.tie (0 ); int t; cin >> t; while (t--) { solve (); } return 0 ; }
原题链接
题目大意翻译:
给定一个无向无环图,上面标记了几个节点。找出一个节点到达所有节点的距离最短,输出这个节点到达最远一个标记节点的距离。
例如:
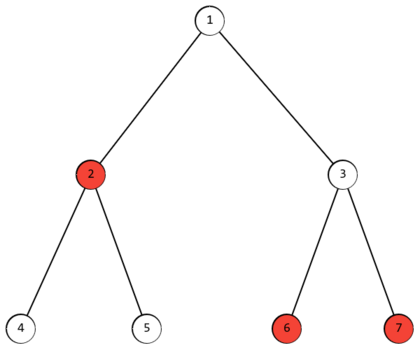
在这个图中2,6,7是标记节点,根据计算可以得出节点1或节点3到达最远标记节点的距离最小。
①到达最远的标记节点是⑥和⑦,距离为2。
③到达最远的标记节点是②,距离为2。
我们首先从任意一个标记 节点v 1 v_1 v 1 标记 节点v 2 v_2 v 2
再从v 2 v_2 v 2 标记 节点v 3 v_3 v 3 v 1 v_1 v 1 v 2 v_2 v 2 v 3 v_3 v 3 d i s t a n c e distance d i s t a n c e
最终答案就是d i s t a n c e 2 \frac{distance}{2} 2 d i s t a n c e
特别的,当只有一个标记节点的时候直接返回0。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 vector<vector<int >> m; void dfs (int v, int past, vector<int >&d) if (past != -1 ) d[v] = d[past] + 1 ; for (int & u:m[v]) { if (u!=past) dfs (u, v, d); } } void solve () int n, k; cin >> n >> k; m.assign (n, vector <int >(0 )); vector<int > mark (k) ; fi (i, 0 , k-1 ) { cin >> mark[i]; --mark[i]; } int a, b; fi (i, 1 , n - 1 ) { cin >> a >> b; a--, b--; m[a].push_back (b); m[b].push_back (a); } if (k == 1 ) { cout << 0 << '\n' ; return ; } vector<int > d1 (n) ; dfs (mark[0 ], -1 , d1); int v2 = mark[0 ]; for (int & num : mark) { if (d1[v2] < d1[num]) v2 = num; } vector<int > d2 (n) ; dfs (v2, -1 , d2); int v3 = mark[0 ]; for (int & num : mark) { if (d2[v3] < d2[num]) v3 = num; } cout << ((d2[v3] + 1 ) >> 1 ) << '\n' ; return ; }